How an SAT question became a mathematical paradox. Head to https://brilliant.org/veritasium to start your free 30-day trial, and the first 200 people get 20%...
I summarized it above, there’s an extra rotation included when the outer circle moves along the inner circle, essentially falling a bit with every roll forward. If the outer circle rolled along a straight line of the same length as the circumference of the inner circle, it would only roll 3 times, but moving around the circle instead adds exactly one extra rotation. That other gent says this is used in calculating orbits too, where you’re also moving forward while constantly falling
I read an article about it. Everybody is doing a shit job of describing what happens. The outer circle naturally makes a full rotation as it travels around the inner one, as the path it follows goes around a full 360°, so that counts as one of the rotations it ends up making, which is in addition to the 3 due to travel around the circumference.
First you said add the radii together, then you gave an example subtracting them, but either way this is incorrect. You divide the larger radius by the smaller radius and add 1
Not quite. With radius 2 and 3 circles, the outer circle would take 2.5 rotations to complete the revolution. You have to set the first circle radius to 1 (divide both radii by the lesser) and then add the radii to calculate the relative circumference of the circle drawn by the motion of the center of the outer circle, so the answer would be calculated like:
Watch the video, it’s explained.
deleted by creator
This should have been an article. What’s the summary?
I summarized it above, there’s an extra rotation included when the outer circle moves along the inner circle, essentially falling a bit with every roll forward. If the outer circle rolled along a straight line of the same length as the circumference of the inner circle, it would only roll 3 times, but moving around the circle instead adds exactly one extra rotation. That other gent says this is used in calculating orbits too, where you’re also moving forward while constantly falling
I read an article about it. Everybody is doing a shit job of describing what happens. The outer circle naturally makes a full rotation as it travels around the inner one, as the path it follows goes around a full 360°, so that counts as one of the rotations it ends up making, which is in addition to the 3 due to travel around the circumference.
thank you, that was the comment that explained it for me
Thanks for letting me know! It was too frustrating to not share.
Add the radius together. If the circle is inside. B-A 3-1 = 2.
Does not compute
It’s in the video.
A circle with a radius of 2 and a circle with a radius of 3 would be 5 rotations.
First you said add the radii together, then you gave an example subtracting them, but either way this is incorrect. You divide the larger radius by the smaller radius and add 1
Not quite. With radius 2 and 3 circles, the outer circle would take 2.5 rotations to complete the revolution. You have to set the first circle radius to 1 (divide both radii by the lesser) and then add the radii to calculate the relative circumference of the circle drawn by the motion of the center of the outer circle, so the answer would be calculated like:
2/2 + 3/2 = 5/2 = 2.5
Removed by mod
…?
Its not even remotely what you said. Its A/B+1 or A/B-1 for an interior loop.
edit: I didn’t need to be this aggressive. It’s VAGUELY what you said. its (A+B)/B. You have missed the /B part… which is A/B + 1.
in the example you gave, for radius 2 and 3… it would be 3/2 + 1 or 2.5. Not 5 (off by a factor of 2 because /B)
They explain multiple ways to do it in the video. A circle with a radius of 2 and a circle with a radius of 3 would be 5.
No they don’t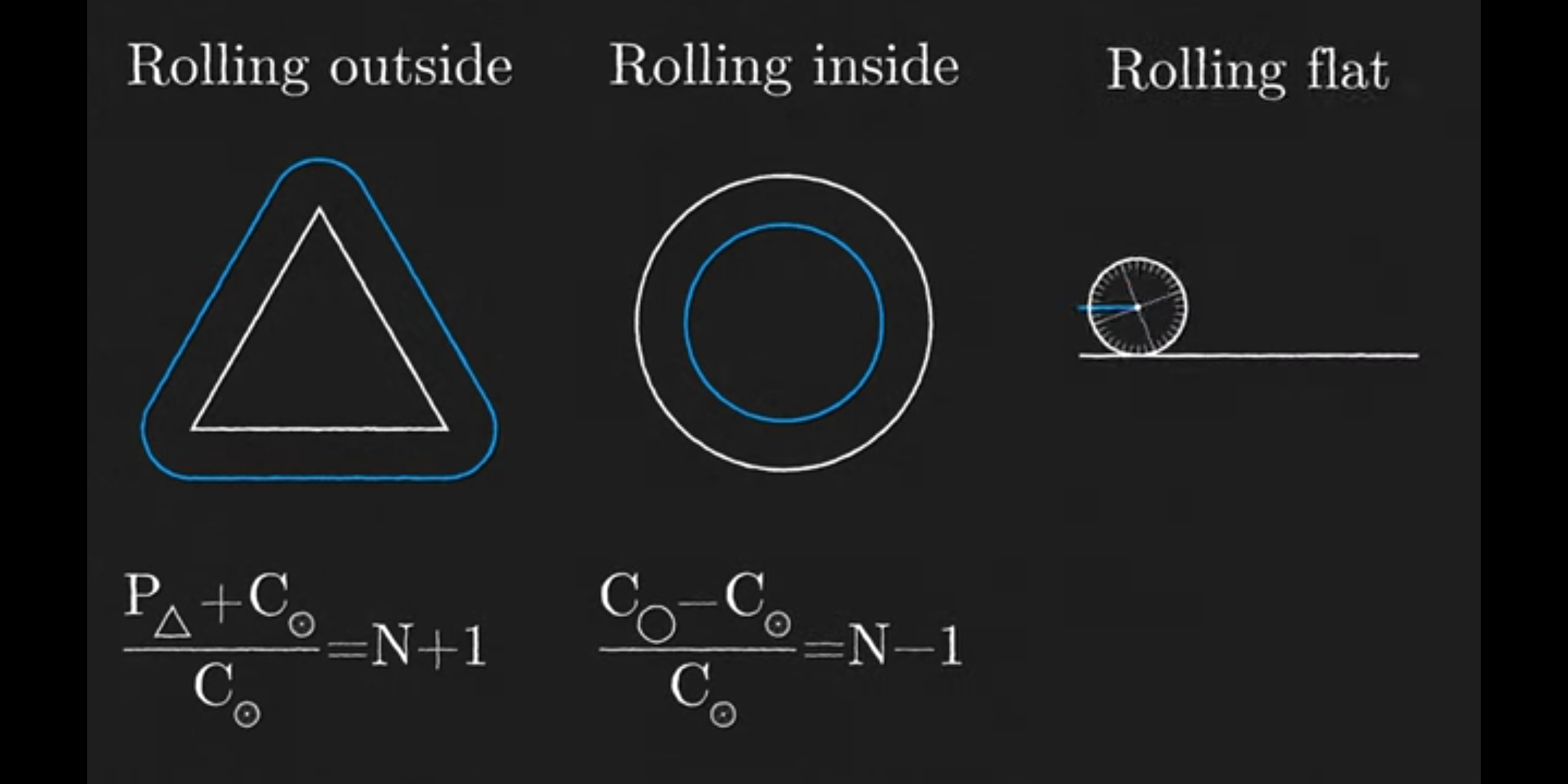
N is the ratio of the circles and its just +1 or -1 depending on outer or inner.