-3 feels like cheating.
Eh, not really. It’s been a while, but I’m pretty sure the rule in algebra when solving for a squared variable like this is to use ± for exactly that reason.
just wait for n-th roots of imaginary numbers :)
-3 id the hidden dark version character of the solution, like evil ryu or devil jin.
just a glimpse into my dark and twisted mind
But for the Joker, that’s the real solution.
i think its more complex than that
Doesn’t x also equal -3?
You found the other
Now kiss
🎶 I was made for solving you baby 🎶
Sqrt(9)
Uhm, actually 🤓☝️!
Afaik sqrt only returns positive numbers, but if you’re searching for X you should do more logic, as both -3 and 3 squared is 9, but sqrt(9) is just 3.
If I’m wrong please correct me, caz I don’t really know how to properly write this down in a proof, so I might be wrong here. :p
(ps: I fact checked with wolfram, but I still donno how to split the equation formally)You’re correct. The square root operator only returns the principal root (the positive one).
So if x^2 = 9 then x = ±√9 = ±3
That’s why in something like the quadratic formula we all had to memorize in school its got a “plus or minus” in it: -b ± √…(etc)
Thanks, I haven’t connected the dots to that (±) sign and this problem.

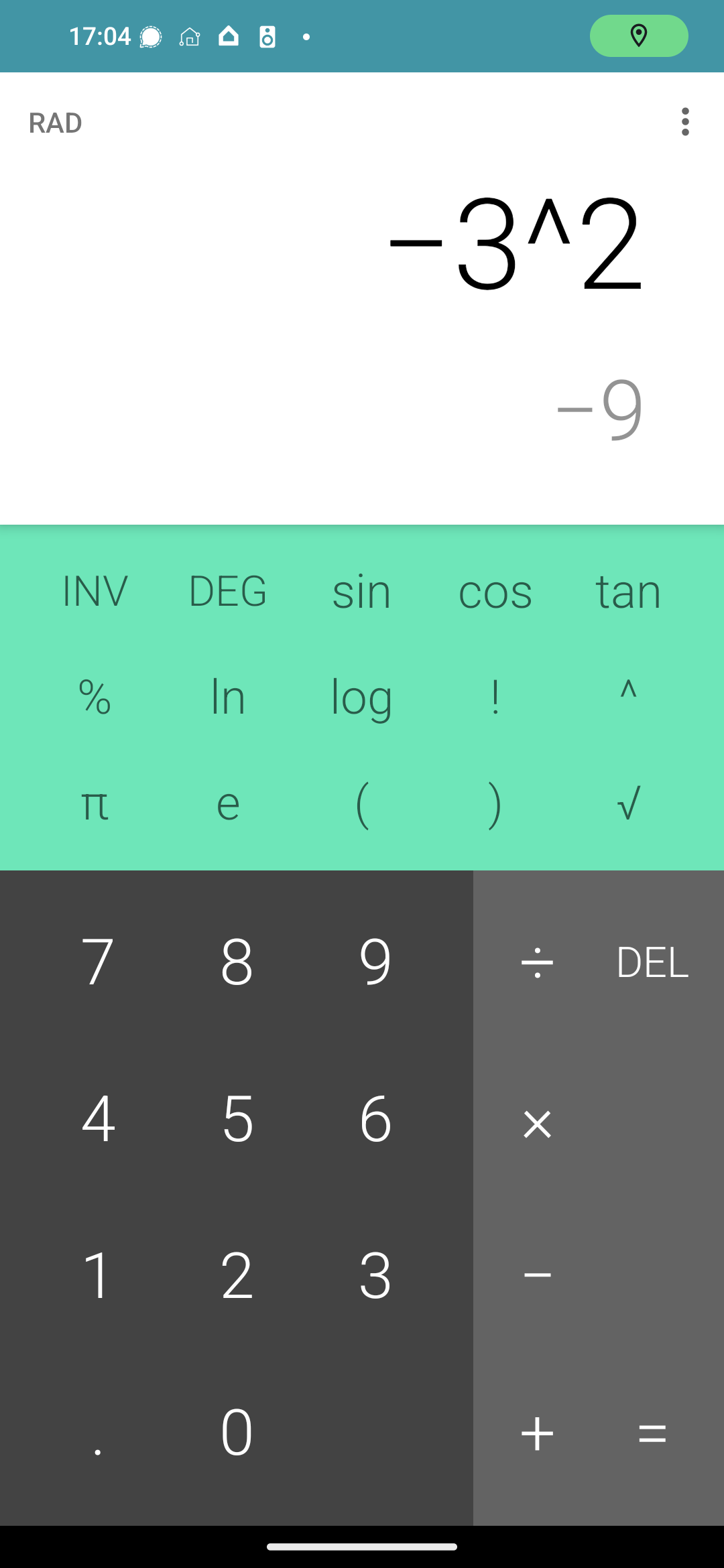
So I checked this on my smartphone first, and thought maybe the software is just shit… So then I checked it on a Casio scientific calc, and both agree.
-3^2 = -9… And 9 != -9
… Are all the calculators somehow wrong? What’s the math rule I’m forgetting here…
I think your calculator is interpreting that as -(3^2) and not (-3)^2
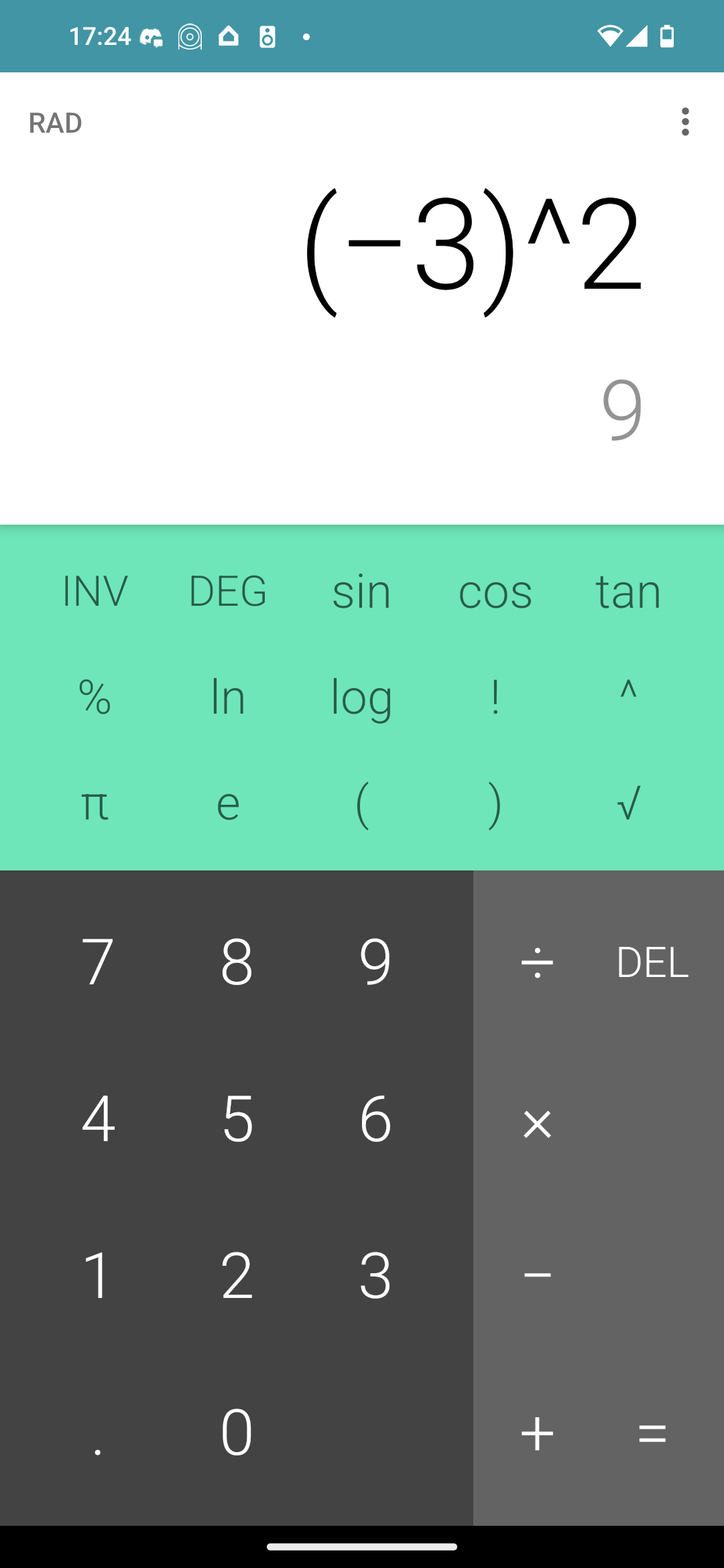
Oh derp. Yep it is.
Was better when calcs had a +/- button.
And I remembered the math rule too.
GD I am just realizing how long its been since I did math in my head without a programming language…
I should take a math class again or something and refresh that knowledge.
x^2 = 9
<=>
|x| = sqrt(9)
would be correct. That way you get both 3 and -3 for x.
That’s the way your math teacher would do it. So the correct version of the statement in the picture is: “if x^2 = 9 then abs(x) = 3”
Cool! Makes sense to me. Honestly, I’ve never done it this way, but it’s so clean. Love it. Thanks.
Fund the sqrter!
Sqrt
hehe
Also math teacher…
“Show your work”
Middle school math memes
The number of solutions/roots is equal to the highest power x is raised to (there are other forms with different rules and this applies to R and C not higher order systems)
Some roots can be complex and some can be duplicates but when it comes to the real and complex roots, that rule generally holds.
I think you can make arbitrarily complicated roots if you move over to Gn which includes the R and C roots…
For example the grade 4 blade
(3e1e2e3e4)^2 = 9in G4Complex roots are covered because the grade 2 blade
(e1e2)^2 = -1making it identical toiso Gn (n>=2) includes C.Gn also includes all the scalars (grade 0 blades) so all the real roots are included.
Gn also includes all the vectors (grade 1 blades) so any vector with length 3 will square to 9 because
u^2 = u dot u = |u|^2whereuis a vector.All blades will square to a scalar but blades are not the only thing in Gn so things get weird with the multivectors(sums of different grades). Any blade with grade
n%4 < 2will square to a positive scalar and the other grades will square to a negative, with the abs of the scalar equal to the norm2 of the blade. Can pretty much just make as many roots as you want if you are willing to move into higher dimensional spaces and use a way cooler product.You lost me at “arbitrarily complicated,” sorry.
Lost me at “I think”. I don’t, apparently.
I don’t think therefore I never was
I wish it was that easy! I stopped thinking and I’m still stuck here… Stupid Descartes
I thought this would be related to quaternions, octonions etc. but no, it’s multivectors and wedge products. Very neat, I didn’t know you could use them like that.
Oh no, you were right on the money. In G2 you have two basis vectors
e1ande2. The geometric product of vectors specifically is equivalent touv = u dot v + u wedge v… the dot returns a scalar, the wedge returns a bivector. When you have two vectors be orthonormal like the basis vectors, thedotgoes to 0 and you are just left withu wedge v. Soe1e2returns a bivector with norm 1, its the only basis bivector for G2.e1e2^2 = (e1e2)*(e1e2) = e1e2e1e2A nice thing about the geometric product is its associative so you can rewrite as
e1*(e2e1)*e2… again that middle product is still just a wedge but the wedge product is anti commutative soe2e1 = -e1e2. Meaning you can rewrite the above ase1*(-e1e2)*e2 = -(e1e1)*(e2e2) = -(e1 dot e1)*(e2 dot e2) = -(1)*(1) = -1… Thuse1e2squares to -1 and is the same asi. And now you can think of the geometric product of two vectors asuv = u dot v + u wedge v = a + biwhich is just a complex number.In G3 you can do the same but now you have 3 basis vectors to work with,
e1, e2, e3. Meaning you can construct 3 new basis bivectorse1e2, e2e3, e3e1. You can flip them to bee2e1, e3e2, e1e3without any issues its just convention and then its the same as quaternions. They all square to -1 ande2e1*e3e2*e1e3 = -e2e1e2e3e1e3 = e2e1e2e1e3e3 = e2e1e2e1 = -1which is the same as i,j,k of quaternions. So just like in G2 the bivectors + scalars form C you get the quaternions in G3. Both of them are just bivectors and they work the same way. Octonions and beyond can be made in higher dimensions. Geometric algebra is truly some cool shit.
Then you can extend to arbitrary algebra
To translate: As a child learning math this equates to “ignore math, the explanations don’t explain anything real, they only explain more math.“
“The only explanation is more abstraction with no real world application as far as math class is concerned. Frankly, there’s more application to your own life experience if you focus on language and the arts.”
I’m guessing that you were one of those “I won’t ever use all this math” kind of students?
Boy do I ever use maths at work all the damn time.
And I’m a mechanic
I was one of those students who asked how it would be used, the teachers didn’t do the whole real world application part, and I never needed to go past trig.
I work with engineers and use math like any other human on the planet but really wish mathematics was taught differently to make it more interesting. You hear a PHD candidate talk about the hairy ball problem and the math is interesting. Math class never was.
Or you were just shit at maths and don’t have any idea how useful it is because you avoid it like the plague.
Me, a statistician: “if chi-square equals 9 then chi equals 3… What??”
My teacher explained as sqrt(poop^2) = abs(poop). Yes, he wrote poop on the blackboard.
He should have drawn a pile of poop instead 💩 (preferably without a face)
Oh, I know this one! It’s pi!
What, no. It’s… Eh close enough.
TAU IS BETTER
/obligatory
Help how do i take factorial of pi
-3 = 3
Adding 3 on both sides
3-3=3+3
0 = 6
1•0 = 6
1 = 6/0
1 = inf
Multiplying e^(iπ) on both sides,
e^(iπ) = - inf
iπ = ln|-inf|
π = ln|-inf| ÷ i
1/0 isn’t infinity though.
Like if everything else is true.
1/0 can be infinity as a limiting case but not always. So imma use what i like since i also took ln|x| (took mod out of nowhere just to make it positive)
Division is repeated subtraction. How many times can you subtract 0 from 1?
I gotta say second half of that goes over my head, but I raise my hat to you
I remember you. You saved me from rickroll on xkcd
Damn me
it starts out okay but 6/0 is not inf.
Its just the joke i take watever i want. There is | | inside log which is just made up. 6/x as x->0 is infinity though so i’mma use that
Absolutely.
I know the math but I still feel like I’m out of the loop somehow?
(-3)^2 = 9 as well
There’s nothing more to this than linking the star wars quote to the -3. That’s it lol
Oh okay. Don’t mind me trying to over analyze things.
This only ever got handed down to us as gospel. Is there a compelling reason why we should accept that (-3) × (-3) = 9?
You can look at multiplication as a shorthand for repeated addition, so, for example:
3x3=0 + 3 + 3 + 3 = 9In other words we have three lots of three. The zero will be handy later…
Next consider:
-3x3 = 0 + -3 + -3 + -3 = -9Here we have three lots of minus three. So what happens if we instead have minus three lots of three? Instead of adding the threes, we subtract them:
3x-3 = 0 - 3 - 3 - 3 = -9Finally, what if we want minus three lots of minus three? Subtracting a negative number is the equivalent of adding the positive value:
-3x-3 = 0 - -3 - -3 - -3 = 0 + 3 + 3 + 3 = 9Do let me know if some of that isn’t clear.
This was very clear. Now that I see it, I realize it’s the same reasoning why x^(-3) is 1/(x^3):
2 × -3 = -6 1 × -3 = -3 0 × -3 = 0 -1 × -3 = 3Thank you!
i think this is a really clean explanation of why (-3) * (-3) should equal
9. i wanted to point out that with a little more work, it’s possible to see why (-3) * (-3) must equal 9. and this is basically a consequence of the distributive law:0 = 0 * (-3) = (3 + -3) * (-3) = 3 * (-3) + (-3) * (-3) = -9 + (-3) * (-3).the first equality uses
0 * anything = 0. the second equality uses(3 + -3) = 0. the third equality uses the distribute law, and the fourth equality uses3 * (-3) = -9, which was shown in the previous comment.so, by adding
9to both sides, we get:9 = 9 - 9 + (-3) * (-3).in other words,
9 = (-3) * (-3). this basically says that if we want the distribute law to be true, then we need to have (-3) * (-3) = 9.it’s also worth mentioning that this is a specific instance of a proof that shows
(-a) * (-b) = a * bis true for arbitrary rings. (a ring is basically a fancy name for a structure with addition and distribute multiplication.) so, any time you want to have any kind of multiplication that satisfies the distribute law, you need (-a) * (-b) = a * b.in particular,
(-A) * (-B) = A * Bis also true whenAandBare matrices. and you can prove this using the same argument that was used above.
Same reason that a double negative makes a positive.
Here’s another example:
A) -3 × (-3 + 3) = ?
You can solve this by figuring out the brackets first. -3 × 0 = 0
You can also solve this using the distributive property of multiplication, rewriting the equation as
A) -3 × (-3 + 3) = 0
(-3 × -3) + (-3 × 3) = 0
(-3 × -3) - 9 = 0
(-3 × -3) = 9If (-3 × -3) didn’t equal 9 then you’d get different answers to equation A depending on what method you used to solve it.











